Python – رگرسیون خطی (Linear Regression)
رگرسیون
در یادگیری ماشین و مدلسازی آماری، واژه “رگرسیون” زمانی استفاده میشود که بخواهیم رابطه بین متغیرها را پیدا کنیم. این رابطه برای پیشبینی نتایج آینده استفاده میشود.
رگرسیون خطی
رگرسیون خطی از رابطه بین نقاط داده برای رسم یک خط مستقیم استفاده میکند. این خط میتواند برای پیشبینی مقادیر آینده مورد استفاده قرار گیرد.
چگونه کار میکند؟ پایتون متدهایی برای پیدا کردن رابطه بین نقاط داده و رسم خط رگرسیون خطی دارد. به جای استفاده از فرمولهای ریاضی، میتوانیم از این متدها استفاده کنیم.
در مثال زیر، محور x نمایانگر سن و محور y نمایانگر سرعت است. ما سن و سرعت 13 خودرو را هنگام عبور از یک ایستگاه عوارض ثبت کردهایم. بیایید ببینیم آیا دادههای جمعآوری شده میتوانند در رگرسیون خطی استفاده شوند:
مثال
ابتدا نمودار پراکندگی را رسم کنید:
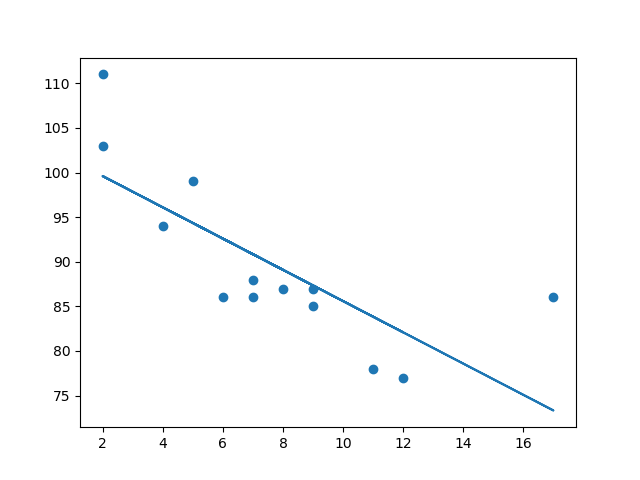
import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()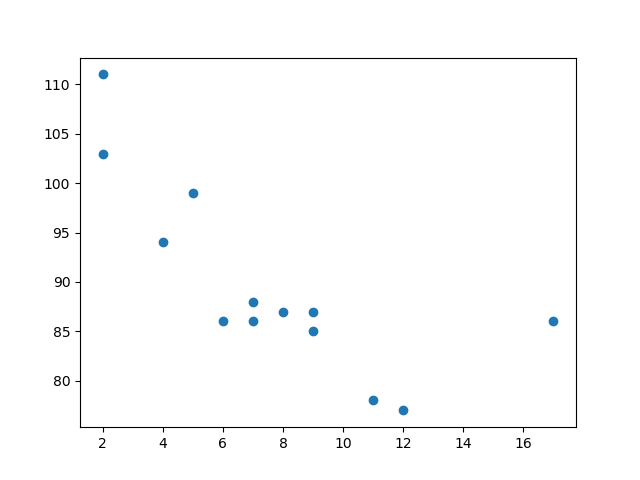
مثال ماژول scipy را وارد کنید و خط رگرسیون خطی را رسم کنید:
import matplotlib.pyplot as plt
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()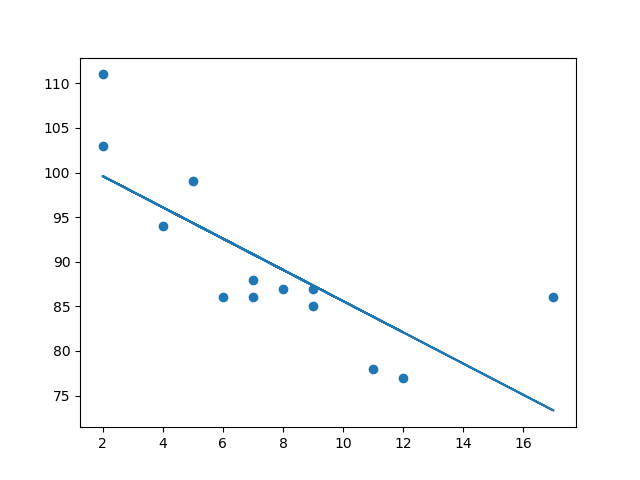
توضیح مثال
- ماژولهای مورد نیاز را وارد کنید:
import matplotlib.pyplot as plt
from scipy import stats- آرایههای
xوyرا ایجاد کنید:
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]- متدی را اجرا کنید که مقادیر کلیدی رگرسیون خطی را برمیگرداند:
slope, intercept, r, p, std_err = stats.linregress(x, y)- تابعی ایجاد کنید که از مقادیر شیب و عرض از مبدأ برای برگرداندن مقدار جدید استفاده کند:
def myfunc(x):
return slope * x + intercept- هر مقدار از آرایه
xرا از طریق تابع اجرا کنید تا آرایهای جدید با مقادیر جدید برای محور y به دست آورید:
mymodel = list(map(myfunc, x))- نمودار پراکندگی اصلی را رسم کنید:
plt.scatter(x, y)- خط رگرسیون خطی را رسم کنید:
plt.plot(x, mymodel)- دیاگرام را نمایش دهید:
plt.show()R برای رابطه
مهم است که بدانید رابطه بین مقادیر محور x و مقادیر محور y چگونه است. اگر رابطهای وجود نداشته باشد، رگرسیون خطی نمیتواند برای پیشبینی استفاده شود. این رابطه – ضریب همبستگی – با r نمایش داده میشود.
مقدار r از -1 تا 1 متغیر است، که 0 به معنی عدم رابطه و 1 (و -1) به معنی 100% رابطه است.
مثال چقدر دادههای من در رگرسیون خطی مناسب هستند؟
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)نتیجه -0.76 نشان میدهد که رابطهای وجود دارد، هرچند کامل نیست، اما نشان میدهد که میتوان از رگرسیون خطی برای پیشبینیهای آینده استفاده کرد.
پیشبینی مقادیر آینده
اکنون میتوانیم از اطلاعاتی که جمعآوری کردهایم برای پیشبینی مقادیر آینده استفاده کنیم.
مثال: بیایید تلاش کنیم سرعت یک خودرو 10 ساله را پیشبینی کنیم. برای این کار، نیاز به همان تابع myfunc() از مثال بالا داریم:
def myfunc(x):
return slope * x + interceptمثال پیشبینی سرعت یک خودرو 10 ساله:
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
speed = myfunc(10)
print(speed)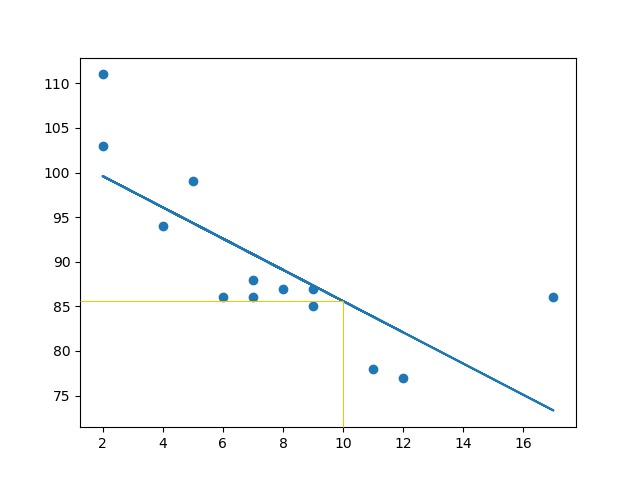
این مثال سرعت 85.6 را پیشبینی میکند که میتوانیم آن را از دیاگرام نیز ببینیم.
مناسب نبودن تطابق
بیایید مثالی بسازیم که در آن رگرسیون خطی روش مناسبی برای پیشبینی مقادیر آینده نباشد.
مثال این مقادیر برای محور x و y باید منجر به تطابق بسیار بدی برای رگرسیون خطی شوند:
import matplotlib.pyplot as plt
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()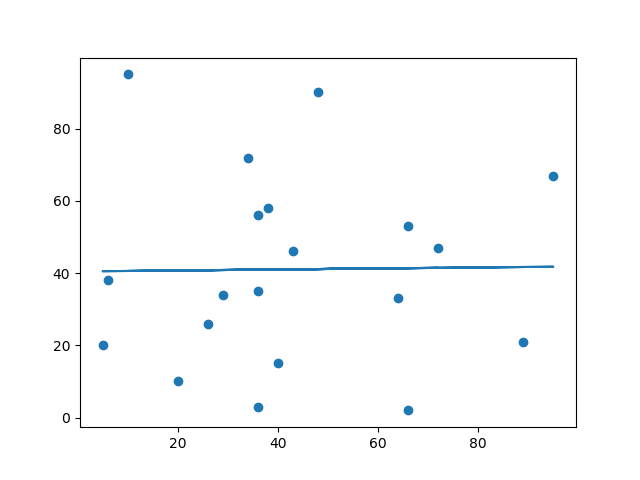
و مقدار r برای رابطه؟ مثال باید مقدار r بسیار پایینی دریافت کنید:
import numpy
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)نتیجه: 0.013 نشان میدهد که رابطه بسیار ضعیف است و به ما میگوید که این مجموعه داده برای رگرسیون خطی مناسب نیست.






برای ارسال نظر لطفا ابتدا وارد حساب کاربری خود شوید. صفحه ورود و ثبت نام